Les carrés existent-ils ? Promenade géométrique, d’Euclide à Einstein

Il y a environ 2300 ans, Euclide, mathématicien grec, posa les bases de la géométrie plane telle qu’on l’enseigne encore en primaire et secondaire. Par une approche très rigoureuse de sa matière, il montra que la géométrie peut reposer sur quelques axiomes (définissant les objets géométriques tels que droites et points) et cinq postulats.

Euclide et les bases de la géométrie plane

Aujourd’hui, ces postulats nous paraissent évidents. Le premier, par exemple, énonce qu’il existe une unique droite passant par deux points donnés. Le cinquième affirme^[1] : « Etant donné une droite D et un point M extérieur à cette droite, il ne passe qu’une parallèle à D passant par M ». A partir de ces quelques « règles du jeu », on peut démontrer tous les résultats usuels de géométrie de primaire et secondaire, par exemple : « Il existe une figure fermée à quatre angles droits et quatre côtés égaux, nommée carré », ou « La somme des angles d’un triangle vaut 180 degrés ». Cela pourrait paraître de la « pédanterie mathématique », selon la formule du physicien Penrose^[2], de s’inquiéter de faits qui nous paraissent aussi évidents que l’existence du carré. Après tout, il suffit de le tracer avec une latte! Pourtant, nous allons voir qu’Euclide s’est montré extraordinairement visionnaire en prenant ces précautions.

Le mystérieux cinquième postulat 

Revenons sur le cinquième postulat. L’énoncé « Etant donné une droite D et un point M extérieur à cette droite, il ne passe qu’une parallèle à D passant par M » paraît aller de soi. Pensons à des rails de train : si un rail D et une traverse sont déjà posés, comment poser le deuxième rail, parallèle au premier et passant par l’extrémité M de la traverse? Le cinquième postulat nous dit qu’on n’a pas le choix. Il n’y a qu’une façon de placer un rail parallèle à un rail donné et passant par un point donné. L’évidence même! Pendant des centaines d’années, des mathématiciens se sont posés la question suivante : le cinquième postulat peut-il être déduit des autres (donc prouvé)? Ou bien est-il indépendant des autres (donc indémontrable à partir de ceux-ci)? C’est la seconde option qui a été démontrée : le cinquième postulat est indépendant. On a donc le choix entre deux options. Soit poser comme vrai le cinquième postulat, et faire alors de la géométrie euclidienne, la géométrie ordinaire que nous connaissons : celle où le carré (quatre angles droits et quatre côtés de même longueur) existe. Ou bien, puisque ce postulat est indépendant des autres, on peut avoir l’idée étrange de faire de la géométrie sans lui. On peut même avoir l’idée extraordinaire de tourner le dos à l’évidence et de fonder une géométrie nouvelle en remplaçant le fameux postulat par sa négation : « Pour toute droite D et un point M différent de D, il passe par M au moins deux parallèles à D ». On mesure difficilement le courage nécessaire pour oser une affirmation si étrange. Plusieurs parallèles à une droite D passant par M ? Non-sens (pensons aux rails)! Gauss, malgré sa notoriété de plus grand mathématicien du 19^e siècle, répugnait à évoquer cette partie de ses recherches, de crainte d’une polémique^[3]. Et pourtant, les mathématiciens Gauss et Bolyai, entre autres, ont bâti une géométrie « non-euclidienne » basée sur ce postulat bizarre. Dans cette géométrie, difficile à appréhender car on ne peut pas la dessiner directement (mais seulement en faire des représentations indirectes^[4]), le carré, figure fermée à 4 angles droits et 4 côtés égaux, n’existe pas, et la somme des angles d’un triangle ne vaut jamais 180 degrés!

Et dans le monde réel?

On pourrait objecter : « Les mathématiciens s’amusent, en refusant le cinquième postulat, à  créer un monde étrange. Mais on voit bien que le monde réel est euclidien, que le carré existe. Alors, ces spéculations peuvent-elles avoir une quelconque utilité pour décrire le monde réel? » De façon spectaculaire, la physique répond par l’affirmative ! Depuis les travaux de relativité générale d’Einstein (1915), parfaitement confirmés par l’observation astronomique sur de très grandes distances, nous savons que le monde est non-euclidien, c’est-à-dire que le cinquième postulat n’y est pas respecté. Nous vivons dans un univers « courbe » où les carrés n’existent pas! Certes, n’importe qui peut tracer un carré sur une feuille de papier : le monde familier est, à toutes fins pratiques, euclidien. Mais, à des échelles de milliards d’années-lumière, une figure fermée à 4 côtés égaux et 4 angles droits n’existe pas! Pour tenter d’approcher cette réalité difficile à imaginer, procédons par analogie.

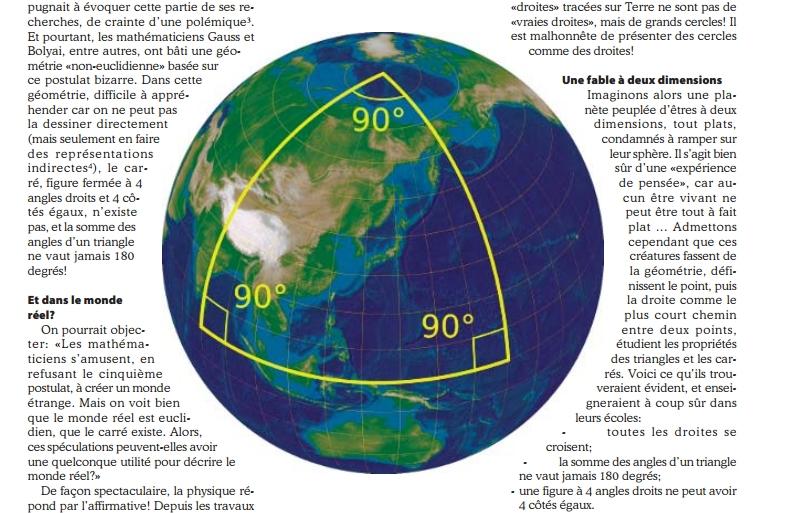
Exemple de géométrie non-euclidienne

Deux avions partent de Belgique, l’un de Bruxelles, l’autre de Liège, les deux en ligne droite et plein Nord. Les deux trajectoires sont parallèles, n’est-ce pas? Pourtant, le premier avion arrive, au bout de 4500 km environ, au pôle Nord. Le deuxième, au bout de 4500 km également, parvient… au pôle Nord, bien sûr. Ces trajectoires ne sont donc pas parallèles puisqu’elles se coupent! Sur une sphère, les droites parallèles n’existent pas! Un de ces avions parcourt un triangle de 10.000 km de côté : il quitte le pôle Nord, parcourt 10.000 km jusqu’au large de l’Inde, puis tourne à angle droit à gauche et parcourt 10.000 sur l’équateur jusqu’au milieu du Pacifique, puis vire de nouveau à gauche à angle droit et vole 10.000 km vers le Nord jusqu’au pôle. Le triangle se referme avec de nouveau un angle droit par rapport à son premier trajet pôle-Inde. Voici donc un triangle avec trois angles droits, dont la somme fait donc 270 degrés (figure). Sur une sphère, la somme des angles d’un triangle ne fait pas 180 degrés ! De même, sur une sphère, le carré, défini comme figure avec quatre angles droits et quatre côtés égaux, n’existe pas. Voilà donc un exemple de géométrie non-euclidienne, appelé géométrie sphérique. Certes, pourrait-on dire, mais ces « droites » tracées sur Terre ne sont pas de « vraies droites », mais de grands cercles! Il est malhonnête de présenter des cercles comme des droites!

Une fable à deux dimensions

Imaginons alors une planète peuplée d’êtres à deux dimensions, tout plats, condamnés à ramper sur leur sphère. Il s’agit bien sûr d’une « expérience de pensée », car aucun être vivant ne peut être tout à fait plat … Admettons cependant que ces créatures fassent de la géométrie, définissent le point, puis la droite comme le plus court chemin entre deux points, étudient les propriétés des triangles et les carrés. Voici ce qu’ils trouveraient évident, et enseigneraient à coup sûr dans leurs écoles :

• toutes les droites se croisent;
• la somme des angles d’un triangle ne vaut jamais 180 degrés;
• une figure à 4 angles droits ne peut avoir 4 côtés égaux.

Si, sur cette planète, un Euclide proposait la notion de droite parallèle, de carré, ou un postulat  selon lequel « par un point donné M extérieur à D il passe toujours une parallèle à D », ses collègues le prendraient pour un déséquilibré - ou un mathématicien extrêmement novateur, comme Bolyai sur notre Terre. Les mathématiciens de cette planète auraient beaucoup de mal à dire : « En réalité, nous vivons sur une sphère, il se peut que dans d’autres géométries le carré existe », car le concept de « sphère » leur serait étranger. Ils comprendraient difficilement ce qu’un Terrien pourrait leur expliquer : « Votre monde à deux dimensions est courbe. Votre géométrie est différente de la nôtre ».

Refuser l’évidence

Voici donc l’analogie. Nous sommes, dans notre univers à trois dimensions, dans la même situation que les créatures plates dans leur monde à deux dimensions. Nous croyons que notre univers est euclidien, et il nous est très difficile d’imaginer que, sur de très longues échelles de distances, il ne l’est pas : il est « courbe ». Seules des personnes exceptionnellement imaginatives, comme Gauss ou Einstein, ont pu avoir cette idée extraordinaire de se défaire de la géométrie euclidienne, qui semble pourtant si « naturelle ». La rigueur d’Euclide a alimenté les spéculations de mathématiciens des 18^e et 19^e, qui ont inspiré Einstein au 20^e pour bâtir sa théorie d’un univers non-euclidien : un univers où les carrés fermés n’existent pas. Voilà un beau morceau d’histoire des sciences, où, une fois de plus, on apprend qu’une part du génie consiste à ne pas prendre comme évident ce qui semble l’être pour tout le monde.   François Chamaraux, Docteur en physique   ^[1] Rappelons que deux droites sont parallèles si elles ne se coupent pas. ^[2] R. Penrose, The Road to Reality, chap 2, Vintage Books, New York, 2007. ^[3] M. J. Greenberg, Euclidean and Non-euclidean Geometry, Freeman & Co, San Francisco, 1974. ^[4] Ceci peut paraître étrange. Pourtant, la plupart des dessins ne sont que des représentations indirectes, et non la réalité elle-même. On ne peut dessiner d’un coup l’intérieur et l’extérieur d’une maison. Et un dessin de pipe n’est pas une pipe!