
Les mathématiques ont ceci de fascinant qu’elles mettent en lien des faits en apparence totalement disparates. Nous en verrons ici un exemple: en réfléchissant sur les petits-fils des lapins et les grands-mères des abeilles, nous parlerons du fameux nombre d’or, prétendument relié à la beauté et l’harmonie; nous rencontrerons sur notre chemin des apiculteurs kabyles, des tournesols, et même un parti politique français.
La suite des lapins
En 1202, un mathématicien de Pise, Fibonacci, se pose la question suivante: si on enferme un jeune couple de lapins avec de quoi manger, comment va évoluer la population? Il pose pour cela une série d’hypothèses très simplificatrices: 1) les lapins sont immortels; 2) la maturité sexuelle a lieu à un an; 3) chaque couple mature donne tous les ans naissance à un mâle et une femelle immature qui se reproduiront entre eux l’année suivante. Il est amusant de calculer l’évolution de la population (voir schéma). Après un an, toujours un couple; ensuite, il y a deux couples (un vieux et un jeune). Un an plus tard, trois couples; puis cinq couples; puis huit couples. En réfléchissant un peu, nous comprenons avec Fibonacci comment procéder: la population à l’année N est la somme des populations des deux années précédentes: 8 = 5+3, 13 = 8+5 etc. Nous obtenons ainsi la suite: 1, 1, 2, 3, 5, 8, 13, 21, 34, etc. Cette série de nombres, où chaque valeur se calcule en fonction des valeurs précédentes, est un exemple de ce qu’on appelle en algèbre une “suite récurrente”, un important domaine des mathématiques, que Fibonacci commence à explorer avec son calcul de lapins immortels. Calcul fructueux, mais totalement artificiel: les vrais lapins finissent par mourir, et ne font pas chaque année exactement un lapin et une lapine. Une vraie population ne suivra jamais une progression de Fibonacci. Il s’agit d’un jeu mathématique plus qu’une description réaliste, mais c’est ainsi que les mathématiciens font souvent avancer leur discipline! 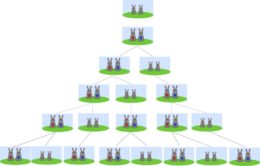
Combien d’ancêtres pour une abeille?
Laissons les lapins tranquilles et considérons le problème suivant: combien d’aïeux une abeille a-t-elle? Quelle drôle de question! Une abeille n’a-t-elle pas 4 grands-parents et 8 arrière-grands-parents, comme tout le monde? Justement, non. Lorsqu’une reine pond un oeuf fécondé, l’insecte venant au monde est une femelle (ouvrière ou reine selon l’alimentation); mais si la reine pond un oeuf non fécondé, c’est un mâle (qu’on appelle faux-bourdon[1]) qui naît. Les féministes en tireront les conclusions qui leur plaisent: chez les abeilles, le mâle a une mère mais pas de père. Cette façon asexuée de se reproduire, la parthénogenèse, existe chez certains animaux (guêpes, pucerons, daphnies, par exemple). Elle n’existe en revanche pas chez les mammifères, même si l’étymologie de parthénogenèse (qui signifie en grec “création vierge”, donc très exactement “conception virginale”) nous rappelle bien sûr une histoire concernant une espèce de primate fort répandue sur Terre[2] . Nous pouvons donc maintenant compter les aïeux d’un faux-bourdon. Une mère, pas de père: 1 parent. La mère a deux parents, donc il y a 2 grands-parents. La grand-mère a deux parents, le grand-père n’a qu’une mère, donc l’abeille a 3 arrière-grands-parents (au lieu de 8 chez l’humain). À l’échelon précédent, nous trouverons 5 (au lieu de 16) arrière-arrière-grands-parents (AAGP), puis 8 AAAGP (au lieu de 32), etc. Nous retrouvons la suite de Fibonacci! Alors que l’arbre généalogique d’un animal habituel (reproduction sexuée telle qu’on la connaît) comprend un nombre d’aïeux en “puissances de 2” quand on remonte les générations (2, 4, 8, 16, 32, 64)[3], le pedigree étrange d’une abeille présente un nombre d’ancêtres en suite de Fibonacci (1, 2, 3, 5, 8, 13).
Les bougies de Bougie
Dans l’Europe chrétienne du 13e siècle, on brûle beaucoup de bougies (qu’on appelle cierges à l’église), à base de cire d’abeille[4]. Où produit-on des bougies à cette époque? À… Bougie, une ville de Kabylie, en Afrique du Nord. Bordeaux produit du bordeaux, Bougie produit des bougies, et Poubelle inventera bientôt la poubelle: tout est à sa place. Les apiculteurs kabyles, à la pointe de leur art, alimentent donc le marché européen du cierge. Des navires chargés de cire traversent la Méditerranée vers l’Italie. Si on admet comme une possibilité qu’en 1202, les éleveurs d’abeilles de Bougie savaient que les faux-bourdons n’avaient pas de père (une observation difficile: dans la science occidentale, la parthénogenèse n’a été mise en évidence qu’au 18e ), que le Nord de l’Italie était un lieu de commerce entre les négociants en cire et les Européens, alors il est possible que Fibonacci ait eu vent de ce fait étonnant. Peut-être s’est-il alors interrogé sur la question de l’arbre généalogique des abeilles, ce qui l’aurait conduit vers sa fameuse suite[5] . Abeilles ou lapins, on ne saura sans doute jamais d’où Fibonacci a tiré son idée, mais il est intéressant de constater qu’une fois de plus une idée scientifique majeure provient de réflexions intelligentes sur de simples questions d’observation de la nature, inspirées par des échanges entre personnes d’activités et d’horizons différentes - commerçants, apiculteurs, mathématiciens. Les scientifiques devraient toujours s’intéresser à beaucoup d’autres choses qu’à leur domaine d’activité!
Du Parthénon à Mélenchon: Sa Majesté le nombre d’or [6]
Reprenons la suite de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, etc. Si on fait le rapport de deux termes successifs, on obtient: 5/3 = 1,67; 8/5 = 1,6; 13/8 = 1,625; 21/13 = 1,615. En poursuivant, on observe que ces fractions se rapprochent d’une valeur particulière, (1+√5)/2, qui vaut environ 1,618. C’est le fameux nombre d’or, noté ϕ. Lorsqu’on fait des mathématiques, on se rend compte que ce nombre apparaît ici ou là, dans la géométrie du pentagone, des polyèdres ou de l’étoile à 5 branches, par exemple, mais aussi dans les structures de certaines fleurs, qui comprennent souvent 5, 8, 13, 21, 34, pétales. L’explication de ce dernier phénomène est intéressante: la disposition de la plante qui optimise la lumière pour chaque bourgeon conduit à ce nombre de pétales. Le résultat est superbe: de splendides structures, comme dans le coeur du tournesol. Pentagones, abeilles, tournesol… c’est intéressant, mais il semble exagéré d’utiliser l’appellation nombre d’or… D’où vient cette dénomination flatteuse? Au 15e , ce nombre est appelé pour la première fois “la divine proportion” par Luca Pacioli, un mathématicien qui, publiant un ouvrage sur le sujet avec Léonard de Vinci, voit dans ce nombre des “attributs qui appartiennent à Dieu”, pour des raisons liées entre autres à ses propriétés géométriques. Au début du 19e siècle apparaissent les noms “section dorée” ou “nombre d’or”. Peu après, au milieu du siècle, un philosophe allemand, Zeising, expose des idées plutôt audacieuses: ϕ ne serait rien moins que la clé de compréhension de la beauté et de l’harmonie, en science et en art! La ruée vers le nombre d’or peut commencer. Tout ce qui est harmonieux, que ce soit en architecture, musique, anatomie, doit contenir le nombre d’or. Des artistes et des philosophes, pensant détenir la clé de la beauté dans un simple nombre, le cherchent dans les proportions du Parthénon, des tableaux de maîtres, du corps humain, etc. On le cherche partout, et on le trouve! La mode du nombre d’or n’est absolument pas retombée de nos jours: la lettre ϕ a été choisie comme symbole du parti français “La France insoumise” de M. Mélenchon, entre autres pour cette raison de symbole d’harmonie[7]. Et on ne compte pas les milliers de publications “prouvant” que le nombre d’or explique tout, de l’ADN aux structures de l’Univers en passant par les Pyramides.
Tout ce qui brille n’est pas nombre d’or!
Cette fièvre du nombre d’or, basée sur l’idée fascinante (mais incroyablement naïve!) que la beauté pourrait se mesurer d’après un seul nombre, ne repose sur rien de très sérieux, pour au moins trois raisons. D’abord, les tenants de cette idée ne citent pas d’article scientifique qui ait montré que des oeuvres respectant des proportions “dorées” soient jugées plus harmonieuses que les autres. On pourrait imaginer, par exemple, une étude où on demanderait à des sujets de donner leur avis sur des rectangles de différentes proportions. Des millions de tableaux présentent un rapport longueur/largeur très différent de 1,618: Les Tournesols, de Van Gogh, que personne ne soupçonne d’être inintéressant vu son prix, possède par exemple un rapport de 1,26. Ensuite, le fait que tel ou tel architecte ou artiste (Le Corbusier, Xenakis, Léonard de Vinci) ait utilisé le nombre d’or dans ses oeuvres ne prouve strictement rien sur la beauté apportée par cette proportion. Cela prouve simplement que la personne en question croyait aux vertus harmonisantes du nombre d’or! Enfin, que l’on mesure un Botticelli, l’ADN ou un prélude de Bach, il est facile de s’apercevoir qu’en cherchant bien, on finit toujours par trouver des rapports de longueurs proches de 1,618. Je m’en aperçois, à ma modeste échelle, en divisant le grand axe de la lunette de mes WC par la diagonale de ma planche à pain, un exemple parmi d’autres qui devrait faire douter de la capacité d’harmonisation de ϕ.
ϕ, un petit nobliau de province
Le nombre d’or apparaît certes dans quelques phénomènes intéressants, des abeilles aux tournesols (les vrais: pas les tableaux de Van Gogh!) en passant par les pentagones et certains polyèdres; mais il ne présente absolument pas l’universalité des deux nombres vraiment extraordinaires des mathématiques, π et e. π, proche de 3,14, défini à partir du périmètre du cercle, apparaît dans tous les domaines des sciences, de l’électricité à la mécanique en passant par la physique des particules et la cosmologie; e, valant environ 2,72, est un nombre ayant à voir avec la croissance exponentielle et la trigonométrie, que l’on retrouve également dans de nombreuses situations. Impossible de faire de la physique ou des mathématiques sans croiser ces deux-là, essentiels à la science. En revanche, ϕ ne doit sa célébrité factice qu’à une prétendue relation, douteuse et non prouvée, avec l’harmonie et la beauté, inventée de toutes pièces au 19e siècle. Bref, avec quelques modestes apparitions géométriques, botaniques et entomologiques, ϕ ne détrônera jamais π et e. À côté de ce couple royal, il ne sera jamais qu’un tout petit nobliau de province!
En conclusion…
Cette petite promenade avec la suite de Fibonacci et le nombre d’or nous a menés dans des lieux variés, de l’Italie à la Kabylie, de l’intimité de la reine des abeilles à un champ de tournesols. Cette tranche d’histoire des mathématiques nous apprend, entre autres choses, que la science commence par la combinaison de l’observation et de la curiosité; que la beauté ou l’harmonie ne se laissent pas définir par quelque chose d’aussi simple que “des rapports de longueur égaux à 1,618” (si l’harmonie était si facile à atteindre, ça se saurait!); et qu’en mathématiques aussi, il y a des effets de mode, des mythes et des croyances.
François Chamaraux, Docteur en physique, enseignant en sciences et mathématiques
[1] Qui ressemble au bourdon; mais le bourdon est une autre espèce [2] On confond souvent la conception virginale de Jésus avec l’Immaculée Conception, qui se rapporte à l’hypothèse selon laquelle Marie serait exempte du péché originel. Certains auteurs rappelant que le Coran mentionne la conception virginale du Christ, pensent même que “l’acceptation de la parthénogenèse a aidé les musulmans à rationaliser la naissance de Jésus comme quelque chose d’inhabituel mais de possible.” www-history.mcs.st-andrews.ac.uk/ Publications/fibonacci.pdf [3] En réalité, en remontant suffisamment haut dans un arbre, nous trouvons toujours des cousins plus ou moins éloignés qui font des enfants ensemble, ce qui réduit le nombre des ancêtres: par exemple 31 au lieu de 32 AAAGP [4] La chandelle, elle, est en suif. [5] www-history.mcs.st-andrews.ac.uk/Publications/ fibonacci.pdf [6] La lettre ϕ est d’ailleurs l’initiale de l’architecte du Parthénon. [7] www.nouvelobs.com/politique/electionpresidentielle-2017/20161017.OBS9922/lagenese-du-phi-de-jean-luc-melenchon.html



